GAMMA (FONCTION)

GAMMA (FONCTION)

Introduites pour la première fois comme nouvelles transcendantes par L. Euler, la fonction gamma et la fonction bêta, qui s’y ramène, sont les plus importantes «fonctions spéciales» étudiées, au fur et à mesure des besoins, depuis le XVIII^e siècle. C’est ainsi que la fonction gamma intervient dans de nombreuses estimations asymptotiques des «grands nombres», en statistique notamment; elle intervient aussi dans la théorie des séries de Dirichlet (cf. théorie analytique des NOMBRES, fonction ZÊTA).

Nous avons choisi ici d’aborder la fonction gamma dans le domaine réel. Appliquant le principe du prolongement analytique (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques d’une variable complexe, chap. 1), on obtient ensuite l’extension au champ complexe de la plupart des formules.

La fonction gamma dans le domaine réel

Une intégration par parties montre facilement que, pour tout entier positif n , on a:

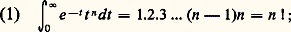mais l’intégrale (1) garde un sens pour des valeurs non nécessairement entières de n , d’où l’idée d’extrapoler ainsi la suite des factorielles. On pose traditionnellement:

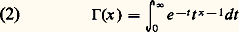(intégrale eulérienne de seconde espèce), forme due à Euler (1781). Pour x 礪 0, cette intégrale est convergente au voisinage de 0, car e ^-t t ^x-1 黎 t ^x-1 pour x tendant vers 0, avec x 漣 1 礪 漣 1; la convergence pour l’infini résulte de la présence du terme exponentiel e ^-t . En fait, on peut montrer que l’intégrale (2) et toutes les intégrales obtenues en dérivant un nombre quelconque de fois par rapport à x sous le signe d’intégration sont uniformément convergentes au voisinage de 0 et de + 秊. La fonction 臨 est donc indéfiniment dérivable pour x 礪 0, de dérivées:

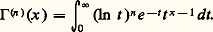Remarquons qu’avec la définition (2) on a, en tenant compte de (1):

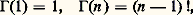ce qui suggère la convention généralement adoptée 0! = 1.

Relation fonctionnelle et graphe

Remplaçant x par x + 1 dans (2) et intégrant par parties, on obtient:

ce qui donne, en faisant tendre a vers 0 et A vers l’infini, la relation fonctionnelle: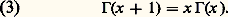

Par récurrence, on en déduit facilement:

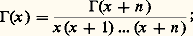cette relation permet de définir 臨(x ) pour x réel négatif, 漣 n 麗 x 麗 漣 n + 1. On a ainsi défini 臨(x ) pour tout nombre réel x qui n’est pas un entier négatif ou nul;

La fonction ln 臨 est convexe sur ]0, + 秊]; en effet, l’inégalité de Schwarz montre que:

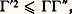d’où (ln 臨) 閭 0. A fortiori, la fonction 臨 est convexe. Comme 臨 (2) = 臨 (1) = 1, la fonction 臨 atteint son minimum sur R⁺ en un point compris entre 1 et 2. La figure 1 représente le graphe de cette fonction.

Formules d’Euler et de Weierstrass

Pour n tendant vers l’infini,

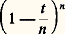tend vers e ^-t pour tout t , et cela suggère la formule (qu’il faut, bien entendu, démontrer rigoureusement):

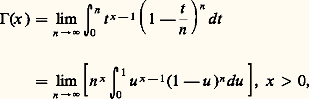la seconde intégrale s’obtenant en faisant le changement de variable t = nu dans la première. Or, un calcul facile montre que:

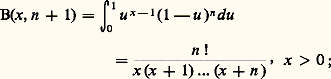d’où la formule d’Euler :

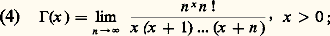Pour transformer cette expression, on peut écrire:

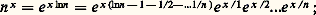or la quantité:

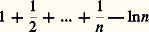tend vers une limite 塚 (la célèbre constante d’Euler 塚 黎 0,577 2) lorsque n tend vers l’infini. Divisant chacun des termes du produit (x + 1)...(x + n ) par l’entier correspondant pris dans n !, on a donc:

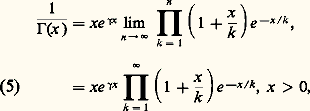puisque le produit infini est convergent ^{[cf. SÉRIES ET PRODUITS INFINIS]}; ce développement en produit infini a été obtenu par Weierstrass.

Comportement asymptotique

Le comportement de la fonction gamma lorsque la variable x tend vers l’infini est décrit par la formule de Stirling :

qui donne, en particulier, un «infiniment grand» équivalent à la factorielle:

on peut d’ailleurs préciser plus étroitement le comportement asymptotique de 臨(x ) (cf. calculs ASYMPTOTIQUES).

Indiquons maintenant une formule due à Legendre pour p = 2 et à Gauss dans le cas général:

formule de Legendre-Gauss :

pour tout entier p 礪 1. Pour p = 2, on a donc:

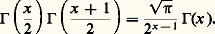Intégrales eulériennes

De nombreuses intégrales définies s’expriment au moyen de la fonction gamma. C’est ainsi que, pour les intégrales eulériennes de première espèce (fonction bêta), x 礪 0 et y 礪 0:

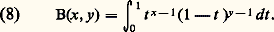À partir de la formule (4), Euler a établi la formule fondamentale:

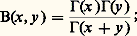on en déduit beaucoup d’autres résultats. Par exemple, si on effectue le changement de variable u = sin² t , on obtient:

Faisant x = y = 1/2 dans la formule précédente, on obtient la valeur:

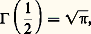qui permet, en utilisant (3), de calculer plus généralement 臨(n + 1/2).

Extension au champ complexe

La formule de Weierstrass (5) garde un sens lorsque la variable x prend des valeurs complexes. En effet, on montre par des majorations que le produit infini de terme général (1 + z /n )e ^-z /n = 1 + u ⁿ (z ) converge normalement (cela signifie que la série de terme général u ⁿ (z ) converge normalement) dans tout disque |z | 諒 R. Ce produit infini définit donc une fonction de z analytique dans tout le plan complexe. Nous poserons par définition :

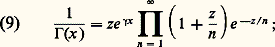cette fonction admet les points 漣 n , n 捻 N, pour zéros simples, et, par suite, la fonction 臨(z ) est méromorphe et ses pôles, simples, sont ces points 漣 n . La formule (9) est la factorisation de Weierstrass de la fonction entière 1/ 臨 (cf. FONCTIONS ANALYTIQUES – Fonctions analytiques d’une variable complexe, chap. 8).

Le principe du prolongement analytique permet alors de voir que de nombreuses formules établies ci-dessus pour x réel positif restent vraies pour z complexe. Par exemple la relation fonctionnelle s’écrit:

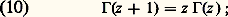la formule (7) de Legendre-Gauss s’étend également. D’autre part, de (9) résulte facilement, en faisant à l’envers le calcul du chapitre 1, que l’on a pour tout z :

où n ^z = e ^{zln n} est fonction entière de z . Enfin, pour tout nombre complexe z de partie réelle strictement positive, on a: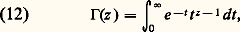

l’intégrale étant uniformément convergente pour 0 麗 a 諒 Re z 諒 M.

La convergence étant normale dans (9), on obtient, en prenant la dérivée logarithmique des deux membres:

pour z 漣 n , n 捻 N, la convergence étant normale sur tout compact de C 漣 (face=F0019 漣N).

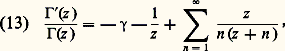La formule des compléments

À partir de (11) et du développement eulérien de sin z (cf. EXPONENTIELLE ET LOGARI- THME, chap. 5):

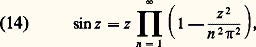on obtient l’importante «formule des compléments» due à Euler:

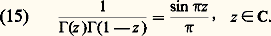Appliquons, par exemple, cette formule pour z = it , t réel. On a alors 臨(1 漣 it ) = 漣 it 臨(face=F0019 漣 it ) = 漣 it 臨(it ) d’après (10), d’où | 臨(it )|² = 神/t sh t .

La formule des compléments peut aussi s’obtenir directement, sans utiliser (13), à partir d’une représentation, due à Hankel, de 1/ 臨(z ) comme intégrale curviligne le long d’un «chemin sans fin»: cette formule (16) sert d’ailleurs dans de nombreuses questions relatives à la fonction gamma.

Désignons par U l’ensemble des nombres complexes privé des réels négatifs ou nuls. Pour z 捻 C et u 捻 U, u ^z désignera la détermination principale de cette fonction dans U, soit u ^z = e ^{zln u} , où ln u représente la détermination principale du logarithme dans U, réelle pour u réel positif. Soit alors L : RU un chemin sans fin dans U défini par L (t ) = r (t )e ^iv(t) , où r (t ) tend vers l’infini lorsque t tend vers 梁 秊, on suppose qu’il existe 﨎 礪 0 tel que:

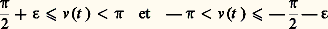au voisinage de + 秊 et de 漣 秊 respectivement (fig. 2). On a alors:

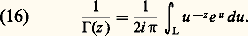Interprétation par la théorie des groupes

Le corps R des nombres réels est localement compact et les caractères du groupe additif R (cf. analyse HARMONIQUE, chap. 4) sont de la forme:

La composante connexe du groupe multiplicatif du corps R est le groupe R⁺, dont la mesure invariante est dt /t . Les caractères du groupe multiplicatif sont de la forme:

Si on cherche à décomposer un caractère additif selon les caractères du groupe multiplicatif, on est conduit à étudier l’intégrale sur R⁺ (transformée de Laplace, appelée aussi transformée de Mellin):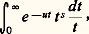

qui converge pour Re s 礪 0 et Re u 礪 0. Le changement de variable ut = x joint à une intégration dans le champ complexe suivant le contour indiqué dans la fig. 2, suivi d’un passage à la limite pour 﨎0 et R+ 秊 (on applique le théorème de Cauchy), conduit à la relation:

où u ^s = exp (s ln u ), en désignant par ln u la détermination principale du logarithme.

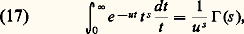Le point de vue précédent montre l’analogie entre la fonction gamma et les sommes de Gauss, en arithmétique, où on considère l’anneau fini Z/n Z des entiers modulo n et le groupe multiplicatif Gⁿ de ses éléments inversibles. Ces deux cas relèvent de l’analyse harmonique dans les anneaux localement compacts (cf. théorie des NOMBRES [nombres algébriques]).

La formule (17) permet en outre d’exprimer les caractères du monoïde multiplicatif N, à savoir: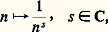

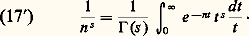à l’aide des caractères t 料 e ^-nt du groupe additif R par la formule:

On en déduit qu’une série de Dirichlet peut s’écrire comme transformée de Mellin d’une série entière:

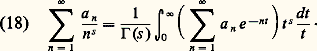La fonction gamma permet ainsi de ramener certains problèmes d’arithmétique multiplicative à des problèmes additifs. En particulier, la célèbre fonction zêta, intervenant dans la théorie des nombres premiers, peut s’écrire sous la forme:

qui est à la base de la théorie de Riemann (cf. fonction ZÊTA).

Encyclopédie Universelle. 2012.